Question 1
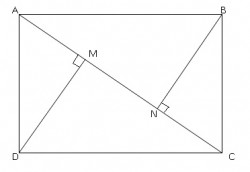
On the rectangle below, the dimensions are 8 cm x 6 cm. BN and DM are perpendicular to diagonal AC. Calculate the length of MN.



Question 2
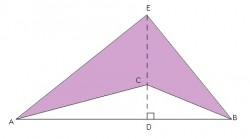
Look at the diagram below. The length of AB is 20 cm and the length of CE is 5 cm. Calculate the shaded area.



View Comments (6)
okay. let the "remained height" as x.
So, the height of larger triangle = 5+x
Thus,
Area of the bigger triangle = 0.5*20*(5+x) = 50+10x
Area of smaller triangle (unshaded) = 0.5*20*x = 10x
Subtract the bigger triangle with the smaller triangle, which gives us:
50+10x-10x = 50 cm^2
what i mean with the height of larger triangle is DE,
"remained height" is CD.
sorry, not paying attention to the question clearly.
Revised:
okay. let the CD as x.
So, DE = 5+x
Thus,
Area of the triangle AEB = 0.5*20*(5+x) = 50+10x
Area of unshaded triangle (triangle ACB)= 0.5*20*x = 10x
Subtract the triangle AEB with triangle ACB, which gives us:
50+10x-10x = 50 cm^2
hehehe...
Okay Josh.......the award goes to youuuu :) for question number 2
Question 1:
Area ABCD = Area ADC + Area ABC
8 x 6 = 0.5 x MD x 10 + 0.5 x BN x 10
48 = 5MD + 5BN
(MD = BN, since ADC congruent to ABC by SSS, they both has the same base, and equally add up to the whole rectangle)
48 = 10 MD
MD = 4.8 = BN
MC =square root (DC squared - DM squared) = sqrt (64 - 23.04) = sqrt 40.96 = 6.4
NC = square root (BC squared - BN squared) = sqrt (36 - 23.04) = sqrt 12.96 = 3.6
MN = MC - NC = 6.4 - 3.6 = 2.8
Question 2:
(Sedang dikerjakan)
Excellent!! and also you can use the formulas obtained from similar triangles that says BC^2 = CN x AC and AB^2 = AN x AC.
And the award goes to youuuu :) for question number 1